Memosa-FVM  0.2
Public Types | Public Member Functions | Private Attributes | List of all members
SquareMatrixESBGK< T > Class Template Reference

#include <SquareMatrixESBGK.h>

Inheritance diagram for SquareMatrixESBGK< T >:
Inheritance graph
[legend]
Collaboration diagram for SquareMatrixESBGK< T >:
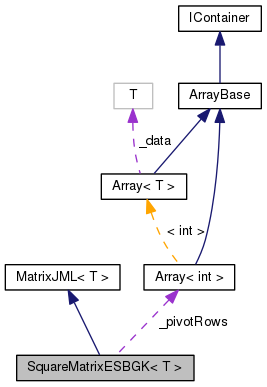
Collaboration graph
[legend]

Public Types

typedef Array< T > TArray
 
typedef Array< int > IntArray
 
typedef NumTypeTraits< T >
::T_Scalar 		T_Scalar
 
- Public Types inherited from MatrixJML< T >
typedef Array< T > TArray
 

Public Member Functions

 SquareMatrixESBGK (const int N)
 
T & getElement (const int i, const int j)
 
T & operator() (const int i, const int j)
 
void zero ()
 
void Solve (TArray &bVec)
 
void makeCopy (SquareMatrixESBGK< T > &o)
 
void printMatrix ()
 
T getTraceAbs ()
 
- Public Member Functions inherited from MatrixJML< T >
 MatrixJML ()
 
virtual ~MatrixJML ()
 
 MatrixJML ()
 
virtual ~MatrixJML ()
 
virtual void multiply (const TArray &x, TArray &b)=0
 

Private Attributes

const int _order
 
const int _elements
 
bool _sorted
 
IntArray _pivotRows
 
TArray _maxVals
 
TArray _values
 

Detailed Description

template<class T>
class SquareMatrixESBGK< T >

Definition at line 14 of file SquareMatrixESBGK.h.

Member Typedef Documentation

template<class T>
typedef Array<int> SquareMatrixESBGK< T >::IntArray

Definition at line 18 of file SquareMatrixESBGK.h.

template<class T>
typedef NumTypeTraits<T>::T_Scalar SquareMatrixESBGK< T >::T_Scalar

Definition at line 19 of file SquareMatrixESBGK.h.

template<class T>
typedef Array<T> SquareMatrixESBGK< T >::TArray

Definition at line 17 of file SquareMatrixESBGK.h.

Constructor & Destructor Documentation

template<class T>
SquareMatrixESBGK< T >::SquareMatrixESBGK ( const int  N)
inline

Definition at line 21 of file SquareMatrixESBGK.h.

References SquareMatrixESBGK< T >::_values, and Array< T >::zero().

21  :
22  _order(N),
23  _elements(N*N),
24  _sorted(false),
25  _pivotRows(N),
26  _maxVals(N),
27  _values(_elements)
28  {_values.zero();}
Array::zero
virtual void zero()
Definition: Array.h:281

Member Function Documentation

template<class T>
T& SquareMatrixESBGK< T >::getElement ( const int  i,
const int  j 
)
inlinevirtual

Implements MatrixJML< T >.

Definition at line 30 of file SquareMatrixESBGK.h.

References SquareMatrixESBGK< T >::_order, and SquareMatrixESBGK< T >::_values.

30 {return _values[(i-1)*_order+j-1];}
template<class T>
T SquareMatrixESBGK< T >::getTraceAbs ( )
inline

Definition at line 184 of file SquareMatrixESBGK.h.

References SquareMatrixESBGK< T >::_order, and fabs().

185  {
186  T trace=0.;
187  for(int i=1;i<_order+1;i++)
188  trace+=fabs((*this)(i,i));
189  return trace;
190  }
fabs
Tangent fabs(const Tangent &a)
Definition: Tangent.h:312
template<class T>
void SquareMatrixESBGK< T >::makeCopy ( SquareMatrixESBGK< T > &  o)
inline

Definition at line 162 of file SquareMatrixESBGK.h.

References SquareMatrixESBGK< T >::_maxVals, SquareMatrixESBGK< T >::_order, SquareMatrixESBGK< T >::_pivotRows, SquareMatrixESBGK< T >::_sorted, and SquareMatrixESBGK< T >::_values.

163  {
164  if(o._order!=this->_order)
165  throw CException("Cannot copy matrices of different sizes!");
166 
167  o._sorted=this->_sorted;
168  o._pivotRows=this->_pivotRows;
169  o._maxVals=this->_maxVals;
170  o._values=this->_values;
171  }
template<class T>
T& SquareMatrixESBGK< T >::operator() ( const int  i,
const int  j 
)
inline

Definition at line 31 of file SquareMatrixESBGK.h.

References SquareMatrixESBGK< T >::_order, and SquareMatrixESBGK< T >::_values.

31 {return _values[(i-1)*_order+j-1];}
template<class T>
void SquareMatrixESBGK< T >::printMatrix ( )
inline

Definition at line 173 of file SquareMatrixESBGK.h.

References SquareMatrixESBGK< T >::_order.

174  {
175  for(int i=1;i<_order+1;i++)
176  {
177  for(int j=1;j<_order+1;j++)
178  cout<<(*this)(i,j)<<" ";
179  cout<<endl;
180  }
181  cout<<endl;
182  }
template<class T>
void SquareMatrixESBGK< T >::Solve ( TArray &  bVec)
inline

Definition at line 34 of file SquareMatrixESBGK.h.

References SquareMatrixESBGK< T >::_maxVals, SquareMatrixESBGK< T >::_order, SquareMatrixESBGK< T >::_pivotRows, SquareMatrixESBGK< T >::_sorted, fabs(), and SquareMatrixESBGK< T >::zero().

35  {//Gaussian Elimination w/ scaled partial pivoting
36  //replaces bVec with the solution vector.
37 
38  SquareMatrixESBGK<T> LU(_order);
39  (*this).makeCopy(LU);
40  IntArray l(_order);
41  TArray s(_order);
42  TArray x(_order);
43 
44  //find max values in each row if not done yet
45  if(!_sorted)
46  {
47  for(int i=1;i<_order+1;i++)
48  {
49  l[i-1]=i;
50  s[i-1]=fabs((*this)(i,1));
51  for(int j=2;j<_order+1;j++)
52  {
53  if(s[i-1]<fabs((*this)(i,j)))
54  s[i-1]=fabs((*this)(i,j));
55  }
56  }
57  _maxVals=s;
58  }
59 
60  //Forward sweep
61  if(!_sorted)
62  {
63  for(int i=1;i<_order;i++)
64  {
65  //T rmax=0;
66  T rmax=fabs(LU(l[i-1],i)/s[l[i-1]]);
67  int newMax=i;
68  for(int j=i+1;j<_order+1;j++)
69  {
70  T r=fabs(LU(l[j-1],i)/s[l[j-1]]);
71  if(r>rmax)
72  {
73  rmax=r;
74  newMax=j;
75  }
76  }
77 
78  /*
79  int temp=l[i-1];
80  l[i-1]=l[newMax-1];
81  l[newMax-1]=temp;
82  */
83 
84  //#pragma omp parallel for
85  for(int j=i+1;j<_order+1;j++)
86  {
87  T factor=LU(l[j-1],i)/LU(l[i-1],i);
88  LU(l[j-1],i)=factor;
89  if(factor!=factor)
90  cout<<"GE NaN at l[j-1], l[i-1], LU(l[j-1],i), LU(l[i-1],i) "<<l[j-1]<<" "<<l[i-1]<<" "<<LU(l[j-1],i)<<" "<<LU(l[i-1],i)<<endl;
91  bVec[l[j-1]-1]-=factor*bVec[l[i-1]-1];
92  for(int k=i+1;k<_order+1;k++)
93  LU(l[j-1],k)=LU(l[j-1],k)-LU(l[i-1],k)*factor;
94  }
95  }
96  _pivotRows=l;
97  _sorted=true;
98  }
99  else
100  {
101  for(int i=1;i<_order;i++)
102  {
103  for(int j=i+1;j<_order+1;j++)
104  {
105  T factor=LU(_pivotRows[j-1],i)/LU(_pivotRows[i-1],i);
106  LU(l[j-1],i)=factor;
107  bVec[_pivotRows[j-1]-1]-=factor*bVec[_pivotRows[i-1]-1];
108  for(int k=i+1;k<_order+1;k++)
109  {
110  LU(_pivotRows[j-1],k)=LU(_pivotRows[j-1],k)
111  -LU(_pivotRows[i-1],k)*factor;
112  }
113  }
114  }
115  }
116 
117 
118 
119  //back solve
120  /*
121  bVec[_pivotRows[_order-1]-1]=
122  bVec[_pivotRows[_order-1]-1]/LU(_pivotRows[_order-1],_order);
123 
124  if(bVec[_pivotRows[_order-1]-1]!=bVec[_pivotRows[_order-1]-1])
125  cout<<"bvec crashes at order"<<endl;
126  T sum=0.;
127  for(int i=_order-1;i>0;i--)
128  {
129  sum=0.;
130  for(int j=i+1;j<_order+1;j++)
131  sum-=LU(_pivotRows[i-1],j)*bVec[j-1];
132  bVec[_pivotRows[i-1]-1]+=sum;
133  bVec[_pivotRows[i-1]-1]=bVec[_pivotRows[i-1]-1]/LU(_pivotRows[i-1],i);
134  if(bVec[_pivotRows[i-1]-1]!=bVec[_pivotRows[i-1]-1])
135  cout<<"GE Error at "<<i<<endl;
136  }
137  */
138 
139  //************back solve***************//
140 
141  //initalize solution vector
142  const T zero(0.);
143  for(int i=0;i<_order;i++)
144  x[i]=zero;
145 
146  x[_order-1]=bVec[_pivotRows[_order-1]-1]/LU(_pivotRows[_order-1],_order);
147 
148  T sum=0.;
149  for(int i=_order-1;i>0;i--)
150  {
151  sum=bVec[_pivotRows[i-1]-1];
152  for(int j=i+1;j<_order+1;j++)
153  sum=sum-LU(_pivotRows[i-1],j)*x[j-1];
154  x[i-1]=sum/LU(_pivotRows[i-1],i);
155  }
156  bVec=x;
157 
158  //***************************//
159 
160  }
fabs
Tangent fabs(const Tangent &a)
Definition: Tangent.h:312
SquareMatrixESBGK::IntArray
Array< int > IntArray
Definition: SquareMatrixESBGK.h:18
template<class T>
void SquareMatrixESBGK< T >::zero ( )
inlinevirtual

Implements MatrixJML< T >.

Definition at line 32 of file SquareMatrixESBGK.h.

References SquareMatrixESBGK< T >::_values, and Array< T >::zero().

Referenced by SquareMatrixESBGK< T >::Solve().

32 {_values.zero();}
Array::zero
virtual void zero()
Definition: Array.h:281

Member Data Documentation

template<class T>
const int SquareMatrixESBGK< T >::_elements
private

Definition at line 194 of file SquareMatrixESBGK.h.

template<class T>
TArray SquareMatrixESBGK< T >::_maxVals
private

Definition at line 197 of file SquareMatrixESBGK.h.

Referenced by SquareMatrixESBGK< T >::makeCopy(), and SquareMatrixESBGK< T >::Solve().

template<class T>
const int SquareMatrixESBGK< T >::_order
private

Definition at line 193 of file SquareMatrixESBGK.h.

Referenced by SquareMatrixESBGK< T >::getElement(), SquareMatrixESBGK< T >::getTraceAbs(), SquareMatrixESBGK< T >::makeCopy(), SquareMatrixESBGK< T >::operator()(), SquareMatrixESBGK< T >::printMatrix(), and SquareMatrixESBGK< T >::Solve().

template<class T>
IntArray SquareMatrixESBGK< T >::_pivotRows
private

Definition at line 196 of file SquareMatrixESBGK.h.

Referenced by SquareMatrixESBGK< T >::makeCopy(), and SquareMatrixESBGK< T >::Solve().

template<class T>
bool SquareMatrixESBGK< T >::_sorted
private

Definition at line 195 of file SquareMatrixESBGK.h.

Referenced by SquareMatrixESBGK< T >::makeCopy(), and SquareMatrixESBGK< T >::Solve().

template<class T>
TArray SquareMatrixESBGK< T >::_values
private

Definition at line 198 of file SquareMatrixESBGK.h.

Referenced by SquareMatrixESBGK< T >::getElement(), SquareMatrixESBGK< T >::makeCopy(), SquareMatrixESBGK< T >::operator()(), SquareMatrixESBGK< T >::SquareMatrixESBGK(), and SquareMatrixESBGK< T >::zero().

The documentation for this class was generated from the following file: